Технология нечеткой логики
|
Нечеткая логика появилась в 1965 в работах Лотфи А. Задэ (Lotfi A. Zadeh). Системы на основе нечеткой логики основаны на использовании нечетких множеств, позволяющих отвести степень принадлежности конкретных физических величин к определенным термам-понятиям. Нечеткая логическая система производит однозначное преобразование вектора входных сигналов в вектор выходных сигналов. Для этого преобразования используется механизм нечеткого вывода, основанный на знаниях, заложенных экспертом (т.е. человеком). Входным и выходным сигналам в нечеткой логической системе соответствуют логико-лингвистические переменные, значения которых определяется термами-множествами. База знаний нечеткой логической системы состоит из продукционных правил, определяющих зависимость между входными и выходными термами-множествами, и функций принадлежности, показывающих степень соответствия реальных величин понятиям, определяемых термами-множествами. Например, пусть имеется входной сигнал скорости V. Определим для логико-лингвистической переменной V три значения: МАЛАЯ, СРЕДНЯЯ и БОЛЬШАЯ. Соответствия между реальными значениями скорости и значениями переменной V определяются по их функциям принадлежности (Рис. 1, а). Таким образом, диапазон скоростей от 0.3 до 0.6 м/с с достоверность 1 относятся к понятию "СРЕДНЯЯ". Скорости 0.2 м/с и 0.7 м/с к понятию "СРЕДНЯЯ" относится с достоверностью 0.5. Скорости 0.1 м/с и ниже, равно как 0.8 м/с и выше, к понятию "СРЕДНЯЯ" не относятся (т.е. достоверность 0). И т.д. 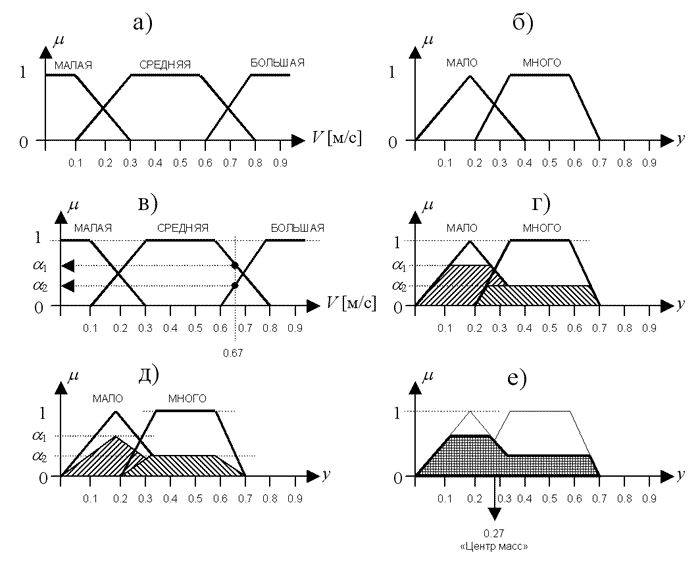 Весь диапазон возможных значений выходной переменной функциями принадлежности разбивают на несколько частей (Рис. 1, б). Удельный вес некоторых выходных функций принадлежности может доминировать над удельным весом других функций принадлежности. Такие функции принадлежности будут доминировать при принятии совместных решений по нескольким правилам. Продукционные правила представляют собой набор инструкций типа: Например: ЕСЛИ V есть СРЕДНЕЕ ТО y есть МАЛО ЕСЛИ V есть БОЛЬШАЯ ТО y есть МНОГО На каждом такте расчета в нечеткой логической системе применяется следующий алгоритм: 1. Фаззификация входных величин (перевод реальных значений в значение логико-лингвистических переменных). 2. Нечеткий логический вывод. 3. Дефаззификация (получение реальных значений выходных переменных). Фаззификация заключается в переводе точных значений входных сигналов в значение логико-лингвистических переменных, используя для этого функции принадлежности. Пусть, например, точное значение сигнала V будет равно 0.67 (Рис. 1, в). Произведем фаззификацию: достоверность понятия "СРЕДНЕЕ" будет равняться a1, достоверность понятия "БЫСТРАЯ" будет a2, а достоверность понятия "МАЛАЯ" будет 0. Нечеткий логический вывод может осуществляться различными методами. Самыми распространенными из них являются метод MAX-MIN и метод MAX-DOT. Оба метода подразумевают последовательную обработку продукционных правил. При обработке каждого правила выполняются следующие действия:
В результате обработки всех правил по каждой выходной переменной образуется совокупность результирующих множеств. Все эти множества объединяются (накладываются друг на друга). После этого осуществляется операция дефаззификации [11, 66] (Рис. 3.1, е), которая заключается в нахождении "центра масс" полученной фигуры. Центр масс рассчитывается по формуле: 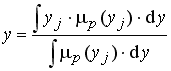 Где: y - выходное значение нечеткой логической системы. Достоинством технологии нечеткой логики является:
На практике возможно два способа применения технологии нечеткой логики. В одном случае используются алгоритмы, производящие нечеткий логический вывод в реальном времени. Во втором случае с нечеткой логической системы снимают входо-выходную характеристику, оптимизируют и записывают в ассоциативную память. Во втором случае достигается максимальное быстродействие системы, даже на самых низкопроизводительных микроконтроллерах. Реализация технологии нечеткой логики специалистами ДинСофтВ компании "ДинСофт" реализован ряд проектов с использованием технологии нечеткой логики. За это время нашими специалистами было разработано все версии графического редактора для настройки базы знаний нечетного регулятора и реализации его процесса логического вывода. Последний вариант оказался более удачным, как по надежности, так и по быстродействию. В настоящее время этот вариант оформлен в виде программного модуля, который компания "ДинСофт" использует в своих программных решениях. Внешний вид программного интерфейса этого модуля представлен на рис. 2. 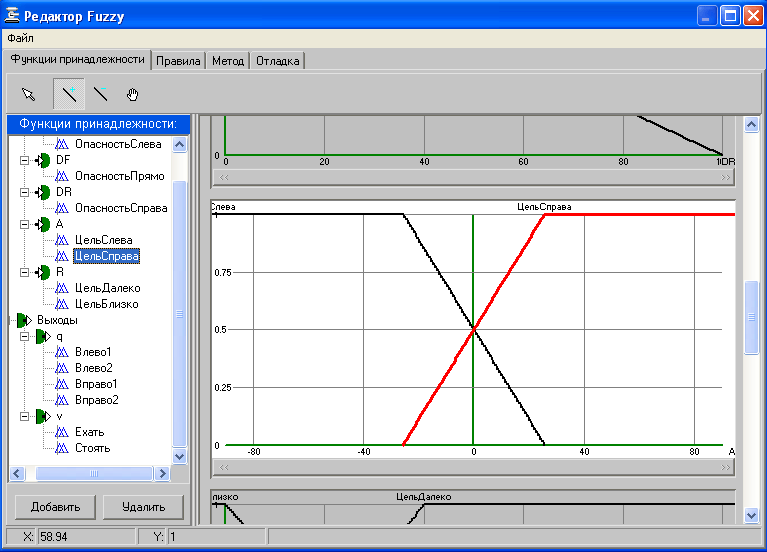 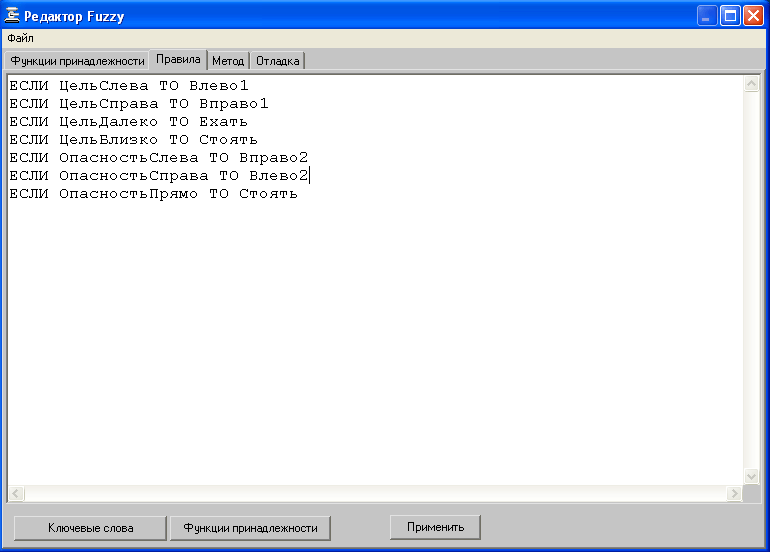 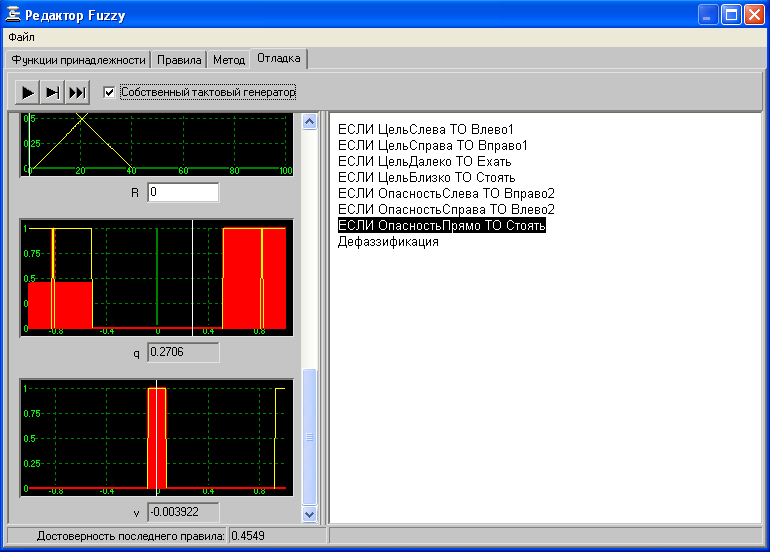 Рис. 2. Внешний вид графического редактора нечеткой логической системы, реализованного в компании ДинСофт |











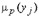 - функция результирующей фигуры;
- функция результирующей фигуры;